べき乗の高速計算 | Revetroniqueのアート探訪

こんばんは、Reveの技術担当です。
今日はべき乗の高速計算でも取り上げようかと。
~~前回、姿勢計測がどうたらとか言ったな、アレは嘘だｗ~~記事にできるほどのクオリティではないので
ここ最近、CodeIQで問題を解いていたりするのですが、その中で数学的な計算の問題が出てきました。
べき乗の計算を高速で処理するプログラムを書くという問題でしたが、~~数学の勉強とかちゃんとしてこなかったのが祟って~~なかなか解けなかったので、自分の備忘録もかねてプログラムの解説をしようかと。
【べき乗】
べき乗とは、同じ数字を任意の回数だけ掛け合わせる計算を意味します。
数式では、Xⁿ というように記述し、Xに任意の数、nに掛け合わせる回数を表記します(2⁵ など)。
一般的にはXのn乗といい、Xを底、nを指数と呼びます。
【実装の問題】
定義としては上の通りなのですが、コンピュータで計算するのには大きな問題を孕んでいます。

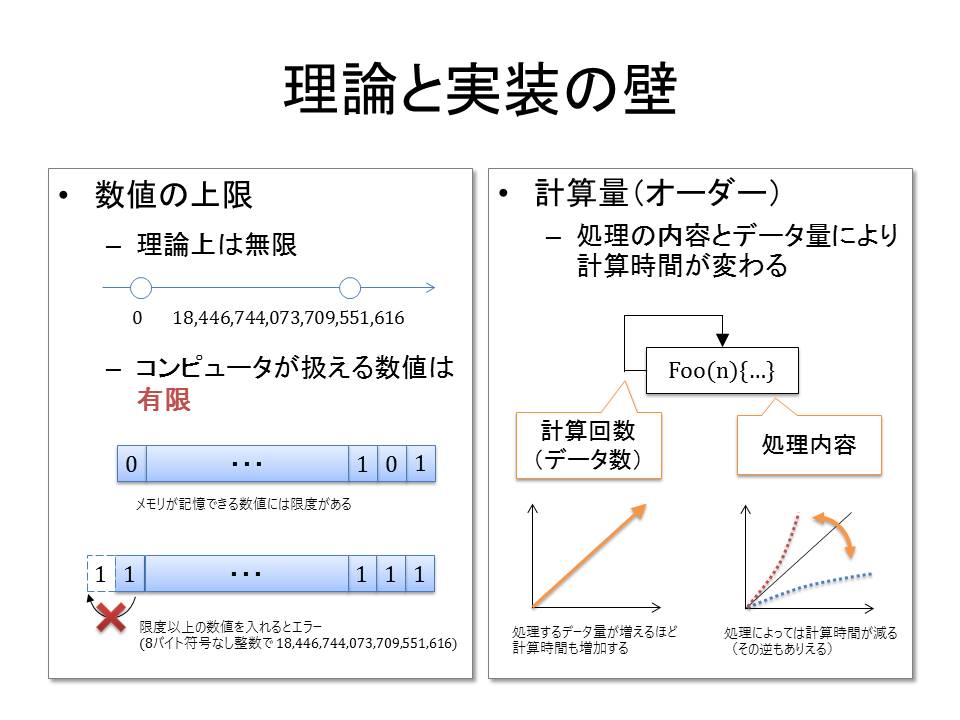
まず、コンピュータが扱える値には限界があるということです。
一般的なプログラミング環境であれば、(言語にもよるが)64ビットの符号なし整数で18,446,744,073,709,551,616がもっとも大きな整数ということになりますが(浮動小数点数は、精度の話などもあるので省略)、これは2を70回かけるだけでも優に超えてしまいます(2の10乗が1024なので、それを7回かければオーバーする)。
今回の問題は下8桁のみを求めるという前提があるので良いのですが、どうにせよ大きな値を扱える変数型を使わなければすぐ桁あふれを起こして問題になるといえます。
さらに問題なのが、単純に計算を繰り返すだけでもコンピュータにとっては負担になる点です。数十回や数百回の計算程度であれば良いのですが、数百万や数千万単位のべき乗となると計算に相当な時間がかかってしまいます。
今回の問題では計算時間に制限(1秒)があり、処理を工夫しないとすぐにタイムオーバーとなります。
【高速計算アルゴリズム】
え、じゃあ計算できても、問題は解けないの…？
とお思いの方もいるかもしれませんが、そんなことはありません。
計算の仕方を工夫することで、プログラムの計算量(オーダー)を減らして短い時間で処理が終わるようにできます。
ここで注目するのは、べき乗の乗数(掛け合わせる回数)。
べき乗を2進数で解釈し、値が1となる桁の場合だけ乗算を行えばよいのです。
(3¹³ = 3⁽¹¹⁰¹⁾ = 3⁽¹⁰⁰⁰⁾ ・3⁽¹⁰⁰⁾ ・3⁽¹⁾ = 6561 ・81・3)

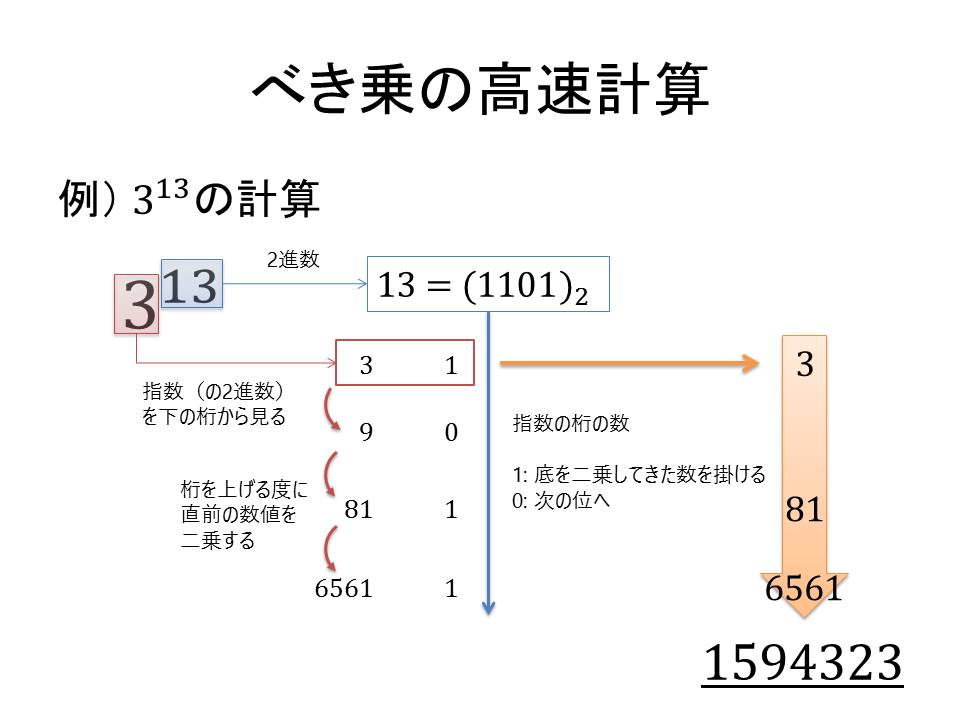
上の例では、そのまま乗算を繰り返すのでは12回計算が必要であるのに対し、先ほどのアルゴリズムを利用すれば6回(位の計算も含めて)で済みます。もちろん、乗数が増えるほど計算量の差は大きくなります。
プログラムでもこのアルゴリズムを実装したいと思います。
【プログラミング】
では、サンプルを見て見ましょう。
今回はC#を使用しています(開発環境は VS Express 2013 for Desktop)。

;  title="RapidPowerCalc.cs"]using System;
namespace RapidPowerCalculate1
{
class Program
{
static void Main(string[] args)
{
for ( ; ; )
{
//標準入力で数値を入れる
//「"底" "指数"」の順番で数値を入れる。2つをスペースで区切ること
//エラー処理は実装していなので注意
String[] temp = Console.ReadLine().Split(' ');
ulong baseVal = ulong.Parse(temp[0]); //べき乗の底
ulong expVal = ulong.Parse(temp[1]);   //べき乗の指数
//入力した数値が二つとも 0 であればプログラムを終了
if(baseVal == 0 &amp;&amp; expVal == 0) //終了
{
Console.WriteLine();
break;
}
//高速べき乗の計算
ulong rslt = 1; //結果を入れる数値。桁あふれを防ぐため、ulong型に変更
while(expVal &gt; 0) //指数が0になるまで
{
if((expVal % 2) == 0) //指数の最下位1ビット: 0
{
baseVal *= baseVal;
baseVal %= 100000000;
expVal &gt;&gt;= 1; //1ビット分だけ右シフト
}
else //指数の最下位1ビット: 0
{
rslt *= baseVal;
rslt %= 100000000;  //下8桁のみを残す
--expVal; //最下位のビットを0にする
}
}
Console.WriteLine(rslt);    //結果を出力
}
}
}
}

; title="RapidPowerCalc.cs"]using System;

namespace RapidPowerCalculate1

{

class Program

{

static void Main(string[] args)

{

for ( ; ; )

{

//標準入力で数値を入れる

//「"底" "指数"」の順番で数値を入れる。2つをスペースで区切ること

//エラー処理は実装していなので注意

String[] temp = Console.ReadLine().Split(' ');

ulong baseVal = ulong.Parse(temp[0]); //べき乗の底

ulong expVal = ulong.Parse(temp[1]); //べき乗の指数

//入力した数値が二つとも 0 であればプログラムを終了

if(baseVal == 0 && expVal == 0) //終了

{

Console.WriteLine();

break;

}

//高速べき乗の計算

ulong rslt = 1; //結果を入れる数値。桁あふれを防ぐため、ulong型に変更

while(expVal > 0) //指数が0になるまで

{

if((expVal % 2) == 0) //指数の最下位1ビット: 0

{

baseVal *= baseVal;

baseVal %= 100000000;

expVal >>= 1; //1ビット分だけ右シフト

}

else //指数の最下位1ビット: 0

{

rslt *= baseVal;

rslt %= 100000000; //下8桁のみを残す

--expVal; //最下位のビットを0にする

}

Console.WriteLine(rslt); //結果を出力

}

プログラムでは、まず標準入力でべき乗の底と指数を入力します。
底と指数はスペースで区切って入力します(間違った形式で入力するとエラーになるので要注意)。
すると、べき乗の計算を上記の手法で計算して標準出力してくれます。
底と指数の両方を0と指定すればプログラムを終了します。
なお、このプログラムでは下8桁しか表示しないように、計算のたびに100000000の剰余算をしていますが、
上の桁の計算結果は下の桁には影響しないため、そのまま切り捨てるために計算しています。
【参考】
こちらのサイトを参考にさせていただきました。
– Security Academia (http://akademeia.info/index.php?%B3%DD%A4%B1%BB%BB%BD%E8%CD%FD#zb9cdf81)
– へなちょここーだー (http://augusuto04.hatenablog.com/entry/2015/05/02/183451)