こんばんは、Reveです。
皆さんお待ちかね、前の記事で取り上げた、行列でのフィボナッチ数列の計算をC#で実装するよ。
そういえばずっとほったらかしでしたね(・ω<)
え、誰も待ってない…だと…。
という茶番は置いといて、さっそく解説に入ります。
【おさらい】
プログラムの前に、考え方を確かめたい方はこちら。
【プログラミング】
では、いよいよプログラミングに取り掛かりましょう。
まずはサンプルを。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 |
; title="Fibonacci.cs"]using System; using System.Collections.Generic; namespace Fibonacci1 { class Program { //2次元行列の積算 //行列a, bの a×b を求める //引数は、行列:a, b、計算する桁数:d static int[,] multMtrx(int[,] a, int[,] b, int d) { //行列の行数と列数 int Ni = a.GetLength(0), Nj = b.GetLength(1), Nk = b.GetLength(0); //多次元配列の長さはGetLengthで求める int[,] rslt = new int[Ni, Nj]; //結果を格納する多次元配列 int dgt = (int)Math.Pow(10, d); //下何桁まで求めるか(10のd乗より下の数まで) //行列bを転置する int[,] bt = new int[Nj, Nk]; for(int i = 0; i < Nk; i++) { for(int j = 0; j < Nj; j++) { bt[i, j] = b[j, i]; } } int sum = 0; //各要素での計算結果を入れる変数 for(int i = 0; i < Ni; i++) //行列aの行数 { for(int j = 0; j < Nj; j++) //行列bの列数 { sum = 0; for(int k = 0; k < Nk; k++) //行列bの行数 { sum += a[i, k] * bt[j, k]; } rslt[i, j] = (sum < dgt) ? sum : (sum % dgt); } } return rslt; } //2次元行列の高速べき乗の計算 //指数部を2進数的に分解して累乗計算する static int[,] powMtrx(int[,] a, int n) { //行列の計算結果の初期化 int[,] rslt = new int[a.GetLength(0), a.GetLength(1)]; //最初は単位行列にしておく for(int i = 0; i < a.GetLength(0); i++) { rslt[i, i] = 1; } //べき乗計算 while(n > 0) { if ((n & 0x01) == 1) rslt = multMtrx(a, rslt, 3); a = multMtrx(a, a, 3); n >>= 1; } return rslt; } static void Main(string[] args) { //入力データの個数 int num = int.Parse(Console.ReadLine()); //求めるフィボナッチ数列の項数 Dictionary<int, int> dat = new Dictionary<int, int>(); for (int i = 0; i < num; i++) { try { dat.Add(i, int.Parse(Console.ReadLine())); } catch(FormatException ex) //入力データの変換エラー { //Console.WriteLine(ex.ToString()); //Console.WriteLine("数値を入力してください"); --i; continue; } } //配列を昇順に並べ替え List<KeyValuePair<int, int>> lst = new List<KeyValuePair<int, int>>(dat); lst.Sort((x, y) => x.Value - y.Value); //ラムダ式で、(前の値 < 後の値)となるように設定 /* //デバッグ用 foreach (KeyValuePair<int, int> pair in lst) { Console.WriteLine("{0} =>{1}", pair.Key, pair.Value); } * */ //行列でフィボナッチ数列の項数を求める //前回の計算結果を記憶しておき、その結果とべき乗の結果を掛け合わせる int[,] initArr = new int[,] { { 1, 1 }, { 1, 0 } }; //フィボナッチ数列の最初 int[,] tempArr = new int[,] { { 0, 0 }, { 0, 0 } }; //途中の計算結果を暫定的に記憶する int[,] fib = new int[,] { { 1, 1 }, { 1, 0 } }; //前回の計算結果 int temp = 0; //前回計算した項 int[] rslt = new int[num]; //計算結果 foreach(KeyValuePair<int, int> pair in lst) { //フィボナッチ数列の計算 tempArr = powMtrx(initArr, pair.Value - temp); //新たに掛け合わせる行列をあらかじめ求める fib = multMtrx(fib, tempArr, 3); //前回の結果と掛け合わせる rslt[pair.Key] = fib[1, 1]; //右下の数値が求める項になる temp = pair.Value; } //計算結果の出力 for(int i = 0; i < num; i++) { Console.WriteLine(rslt[i]); } } } } |
コードが少し長くなってしまいましたので、とりあえず概略から。
このプログラムは、以下の3つから構成されています。
1. 行列の積を計算するメソッド
2. 行列のべき乗を計算するメソッド
3. 指定のフィボナッチ数列の項数を下3桁で求めるメソッド(メインメソッド)
プログラムの流れはこんな感じ
1. メインメソッド内で標準入力(キーボード)から求めるフィボナッチの項を指定。その際、 最初に入力データ数を与え、その後に求める項数を全て入力
2. フィボナッチ数列の計算のため、行列べき乗の計算メソッドを呼び出す(内部で行列の積を求めるメソッドを利用)
3. 指定したすべての項数に対して、上の操作を繰り返してフィボナッチ数列の項を求める
また、行列は多次元配列で表現しています。
C#では、多次元配列と配列の配列(ジャグ配列)は明確に区別されています。
今回は行列の計算であり、行ごとの列数は変わらないので、多次元配列を選びました。
では、それぞれのメソッドについて解説します。
1. 行列の積を計算するメソッド
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
static int[,] multMtrx(int[,] a, int[,] b, int d) { //行列の行数と列数 int Ni = a.GetLength(0), Nj = b.GetLength(1), Nk = b.GetLength(0); //多次元配列の長さはGetLengthで求める int[,] rslt = new int[Ni, Nj]; //結果を格納する多次元配列 int dgt = (int)Math.Pow(10, d); //下何桁まで求めるか(10のd乗より下の数まで) //行列bを転置する int[,] bt = new int[Nj, Nk]; for(int i = 0; i < Nk; i++) { for(int j = 0; j < Nj; j++) { bt[i, j] = b[j, i]; } } int sum = 0; //各要素での計算結果を入れる変数 for(int i = 0; i < Ni; i++) //行列aの行数 { for(int j = 0; j < Nj; j++) //行列bの列数 { sum = 0; for(int k = 0; k < Nk; k++) //行列bの行数 { sum += a[i, k] * bt[j, k]; } rslt[i, j] = (sum < dgt) ? sum : (sum % dgt); } } return rslt; } |
m×l行列とl×n行列をかけて、m×n行列を求めます(2次元行列のみ)。
引数は、任意の2次元行列を二つと、下何桁を求めるかの桁数です(CodeIQで下3桁までという制約があったため)。
なお、1番目の行列の列数と2番目の行列の行数は揃える必要があります(エラー対策はありません)。
処理内容は、まず2番目の行列(B)を転置した行列(Bt)を求めて、それと1番目の行列(A)の積を求めます。
というのも、コンピュータアーキテクチャ的には、アドレスが近い場所にアクセスするほうがより高速に処理できます。
普通に計算すると、後ろの行列(の変数)は飛び飛びに参照しなければなりませんが、転置しておくと隣接した場所を参照して計算できるので、行列の計算ではしばし利用されます。
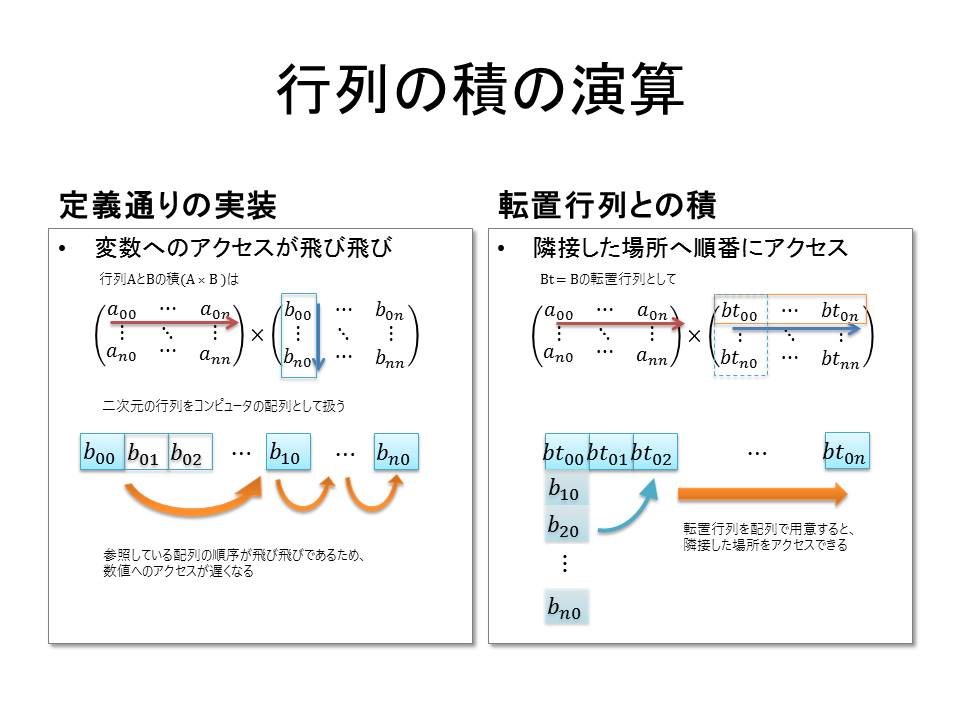
さらに、行列の要素を計算する際も、わざわざ配列にアクセスして足していくよりも、あらかじめ計算結果を別の変数に入れておき、最後に答えを入れる変数に代入するほうが更に処理時間を短縮できます。
(ですが、C#の最適化だとどうなるか、測定してないので分かりませんが(汗)そもそも、.NETのガベージコレクションだとこれが有効かもちゃんとわかってはいませんが…orz)
2. 行列のべき乗を計算するメソッド
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
static int[,] powMtrx(int[,] a, int n) { //行列の計算結果の初期化 int[,] rslt = new int[a.GetLength(0), a.GetLength(1)]; //最初は単位行列にしておく for(int i = 0; i < a.GetLength(0); i++) { rslt[i, i] = 1; } //べき乗計算 while(n > 0) { if ((n & 0x01) == 1) rslt = multMtrx(a, rslt, 3); a = multMtrx(a, a, 3); n >>= 1; } return rslt; } |
1.の行列積を求めるメソッドを使い、任意の行列のべき乗を求めます(もちろん2次元行列のみ)。
引数は、任意の行列とべき乗の指数です。
べき乗の計算に関しては、この記事のように指数を2進数的に分解して処理します。参照の記事では整数でしたが、今回のように行列でも応用できます。

処理としては、まず答えを格納する行列を単位行列(左上から右下の対角線上のみ1、後は0の行列)にしておきます。
指数(の2進数)の各桁ごとに1か0かを調べ、1であれば答えの行列に入力した行列を掛け合わせます。
続いて、入力した行列同士を掛け合わせ、それを入力の行列に戻します。
そして指数を右シフトして、以上の処理を繰り返します。指数が0になれば、処理は終了です。
3. メインメソッド
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
static void Main(string[] args) { //入力データの個数 int num = int.Parse(Console.ReadLine()); //求めるフィボナッチ数列の項数 Dictionary<int, int> dat = new Dictionary<int, int>(); for (int i = 0; i < num; i++) { try { dat.Add(i, int.Parse(Console.ReadLine())); } catch(FormatException ex) //入力データの変換エラー { //Console.WriteLine(ex.ToString()); //Console.WriteLine("数値を入力してください"); --i; continue; } } //配列を昇順に並べ替え List<KeyValuePair<int, int>> lst = new List<KeyValuePair<int, int>>(dat); lst.Sort((x, y) => x.Value - y.Value); //ラムダ式で、(前の値 < 後の値)となるように設定 //行列でフィボナッチ数列の項数を求める //前回の計算結果を記憶しておき、その結果とべき乗の結果を掛け合わせる int[,] initArr = new int[,] { { 1, 1 }, { 1, 0 } }; //フィボナッチ数列の最初 int[,] tempArr = new int[,] { { 0, 0 }, { 0, 0 } }; //途中の計算結果を暫定的に記憶する int[,] fib = new int[,] { { 1, 1 }, { 1, 0 } }; //前回の計算結果 int temp = 0; //前回計算した項 int[] rslt = new int[num]; //計算結果 foreach(KeyValuePair<int, int> pair in lst) { //フィボナッチ数列の計算 tempArr = powMtrx(initArr, pair.Value - temp); //新たに掛け合わせる行列をあらかじめ求める fib = multMtrx(fib, tempArr, 3); //前回の結果と掛け合わせる rslt[pair.Key] = fib[1, 1]; //右下の数値が求める項になる temp = pair.Value; } //計算結果の出力 for(int i = 0; i < num; i++) { Console.WriteLine(rslt[i]); } } |
ここで求めるフィボナッチ数列の項数入力と、計算結果の出力を行います。
まず入力は標準入力(キーボード)で下のように、最初に入力するデータ数、その後に求める項数を入れていきます(項の順番はバラバラでもOK)。なお、数値以外を入力すると直前の操作からやり直しになります。
5
3
128
01000
46
求める項数は、ディクショナリで保管されます(ディクショナリの解説は略)。
ここでは、入力した順番をキー、求める項をバリューとします。
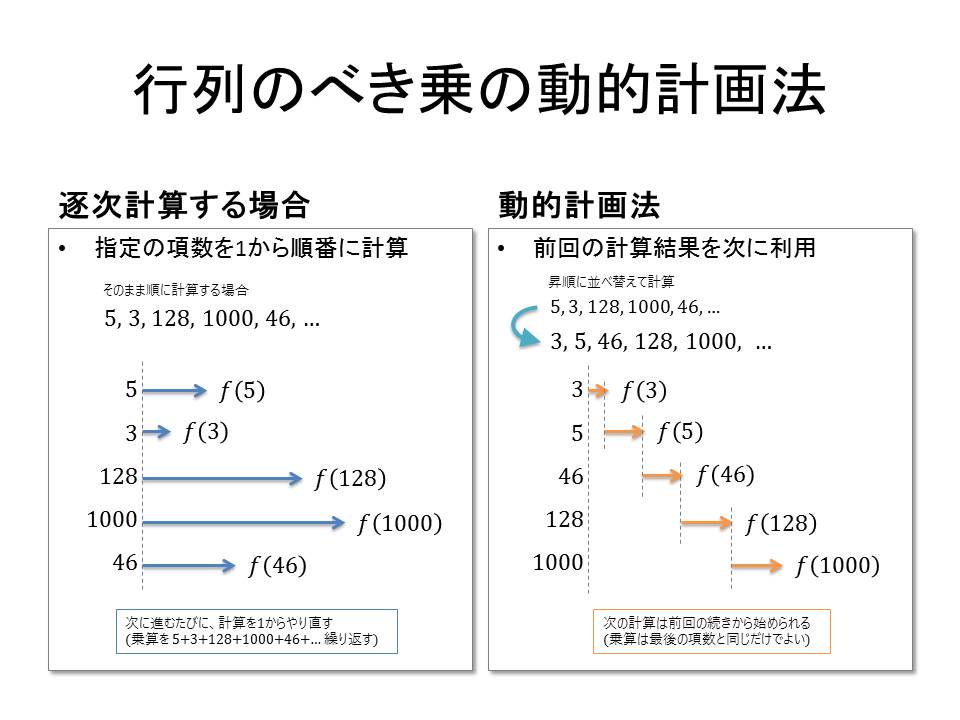
このディクショナリを、項数で昇順に並べ替えます。
すると、前の計算結果を次の計算結果で使えるようになるので(動的計画法)、計算処理数が少なくなります。
では、肝心のフィボナッチ数列の計算に移ります。
フィボナッチ数列の計算用に、2次元配列を3つ(数列の初期行列、途中の計算を一時保存する行列、前回の計算結果)用意しました。数列の計算は、最初の行列をべき乗して求めていきます。
また、前回計算した項と結果の出力用の1次元配列も用意します。
ループはforの代わりにforeachを使いました。
foreachは、ループカウンタを設定する代わりにコレクション(配列、リストなど)の要素を使って繰り返しの処理を行います。
ここでは、先ほどのディクショナリを指定します。
ループ内では、フィボナッチ数列の計算と結果の格納、前回の状態の記録をしておきます。
まず、フィボナッチ数列の計算は新しく掛け合わせる行列を求め(初期行列を (今の項) – (前の項) 分だけかける)、それを前回の計算結果と掛け合わせます。

続いて、計算結果を出力用の1次配列に入れますが、ディクショナリのキーを使ってデータの入力順に並べ替えています。
こうすることで、入力した項に対応して計算結果が出力されます。
そして、次の要素に移る前に今の計算結果と計算した項を記録しておきます。
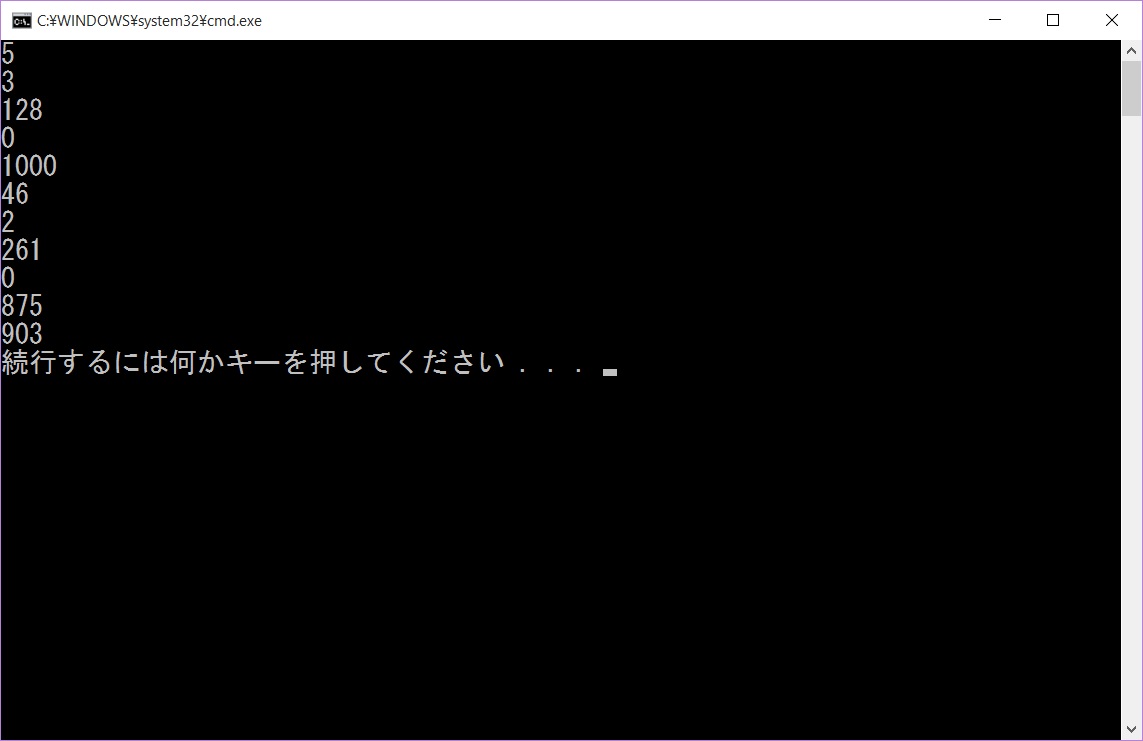
計算の終了後は、結果を標準出力でデータの入力順に出していきます。
プログラムを実行すると、このように計算結果が出力できると思います。
【終わりに】
意外と長くなってしまいましたが、これで計算の解説は終わりです。
学生時代はあまりこうした数値計算は勉強してなかったのですが、やってみると奥が深いですね。
また何かあれば記事にしようかと。
【参考】
こちらのサイトを参考にしました。
projectpn フィボナッチ数の高速計算 (http://www16.atwiki.jp/projectpn/pages/34.html)
TIM Labs フィボナッチ数列の一般項を計算する(※ただし有理数に限る) (http://labs.timedia.co.jp/2012/11/fibonacci-general-term-using-rational.html)
from scratch 動的計画法でフィボナッチ数列の計算を早くする (http://yosuke-furukawa.hatenablog.com/entry/20120120/1327056359)




コメント