こんにちは、Reveです。
常日頃からネタに困っている技術担当です。
今日はどうしようか考えた挙句、プログラムの話になりました。
最近、ちょくちょく「CodeIQ」で問題を解いていたりしますが、
その中でフィボナッチ数列の演算問題が出てきたので、今回は当方のプログラムを載せてみたいと思います。
問題の回答期限はとっくに終了しているので、ネタバレみたいな記事になってもいいよね(・ω<)
【フィボナッチ数列とは】
詳しくは知らなくても、名前くらいは聞いたことがある人も多いでしょう。
イタリアの数学者レオナルド=フィリオ=ボナッチ(レオナルド・フィボナッチ)にちなんで名づけられた数列です(ちなみに、フィボナッチ本人が発見したのではなく、著書で紹介しただけだそうで。あと、本名はレオナルド・ダ・ピサ。へー)
この数列の定義は、3項目以降のある項が前の2つの項の和になるということで、
これを数式で表すと下のようになります。
なお、最初の2つの項は、それぞれ0, 1と与えられます。
F0 = 0
F1 = 1
Fn = Fn-1 + Fn-2 (n > 1)
面白い特徴として、項数が大きくなるほど、ある項とその前の項の比がいわゆる「黄金比」に近い比率となる性質を持ちます。
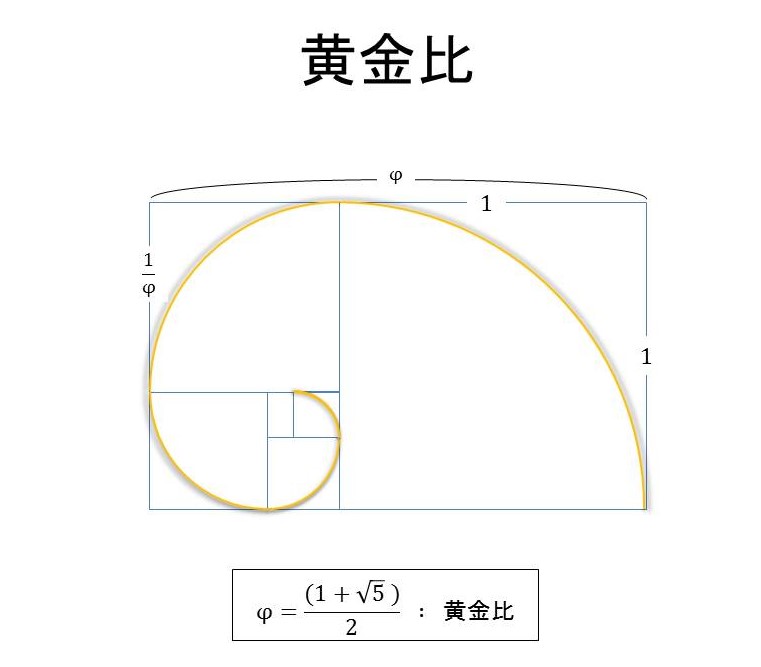
黄金比とは長方形の縦横の比で、ある長方形から短い辺の正方形を切り取った時に、残りの図形の縦横比が元の図形と同じになるような長方形のものを指します。
古代ヨーロッパでは最も美しい長方形の比率と考えられ、自然界にも数多く現れる(花びらの数、カタツムリの螺旋など)ことでも有名です。
【プログラミングでどうするか】
さて、一通り特徴を書いたところで、プログラムを使ってどのように解くかを見ていきましょう。
まず、10~100の位までの小さい項を求めるのであれば、数式の通りに求めていくのも良いでしょう。
1から計算させるより、

直前の計算結果を覚えておいてそれを次の計算結果に使用したほうが処理が断然早くなります(動的計画法)。

ところがっ、CodeIQはそれを許してくれない!何故なら、数千万の位の項を求めさせられるから!!
そして、時間がかかるとタイムアウトするからぁ…残念!!!
計算量が多くて時間のかかる処理は、(たとえ正解にたどり着くとしても)受け付けてくれないんですね。
そのため、高速で処理できる方法を考えます。
フィボナッチ数列の一般項は次の数式で与えられるため、これを計算して整数部を導出する手段も考えられます。
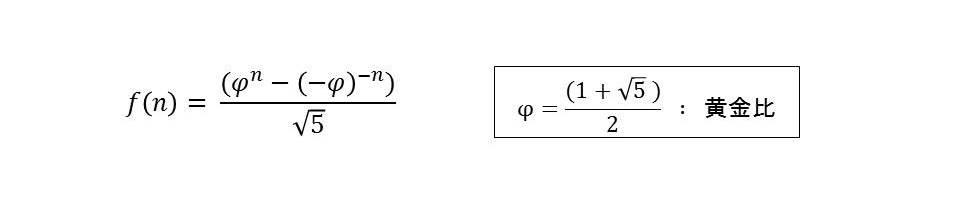
問題は平方根を求める方法とその精度ですが、普通に数学用ライブラリや浮動小数点を使用して計算するには
計算時間はともかく、精度がだいぶ怪しい(100を超えるともう誤差が発生するようです)。
一応、複素数を扱うような形で計算できる(有理数と無理数の計算に分けて、有理数の部分のみ求める)ようですが、当方は別の手段で求めることにしました。それが行列のべき乗算ッ…!!!
【行列での求め方】
フィボナッチ数列を行列で表すと、以下のようになります。
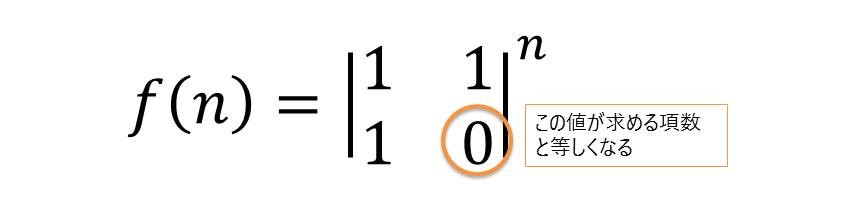
つまり、{{1, 1}, {1, 0}}の2次元行列をN回かければ、求めたい項の値が導出できるのです。
(行列に限らず)べき乗の計算は、普通に乗算すればN回の計算になりますが、少し工夫(この記事を参照)することでlogNのオーダーで求められるようになります。項の位が大きくなるほど効果は歴然と現れます。
【次回は】
と、プログラムまで解説すると長くなってしまうので、実装に関しては次回に持ち越します。次回の更新までに考えてみるのも良いかもしれません(当方の実装より良いものもできると思いますしorz)。
ではまた。
【参考】
こちらのサイトを参考にしました。
projectpn フィボナッチ数の高速計算 (http://www16.atwiki.jp/projectpn/pages/34.html)
TIM Labs フィボナッチ数列の一般項を計算する(※ただし有理数に限る) (http://labs.timedia.co.jp/2012/11/fibonacci-general-term-using-rational.html)
from scratch 動的計画法でフィボナッチ数列の計算を早くする (http://yosuke-furukawa.hatenablog.com/entry/20120120/1327056359)
行列によるフィボナッチ数列の項の計算(1)
 Programming
Programming


コメント